My thesis advisor was Professor Rick Moeckel at the University of Minnesota on the two-body problem in celestial mechanics. I currently work with mathematics professor Michael Green and physics professor Ramin Daghigh at Metropolitan State University, St. Paul. We are researching the gravity waves which emanate from black holes.
Publications
- 2024: Relative Equilibria of Pinwheel Point Mass Systems in a Planar Gravitational Field. (Faculty Supervisor for Ritwik Gaur), Rose-Hulman Undergraduate Math Journal
- 2024: Back to the Books: Navigating Grad School as a Mature Student. MAA’s Math Values Blog
- 2024: Calculating quasinormal modes of extremal and non-extremal Reissner-Nordstrom black holes with May 2024 the continued fraction method. Physical Review D
- 2023: Calculating quasinormal modes of Schwarzschild anti-de Sitter black holes using the continued fraction method. Physical Review D
- 2022: Relative Equilibria of Dumbbells Orbiting in a Planar Newtonian Gravitational System. Thesis
- 2020: Scalar perturbations of a single-horizon regular black hole. Physical Review D
- 2020: Significance of black hole quasinormal modes: A closer look. Physical Review D
- 2016: The Consequence of Using a Quantum Two-State Magnetic Field in a Stern-Gerlach Experiment. Preprint
- 2014: Environmental sustainability curriculum for college algebra and pre-calculus. Engaging Mathematics
Two-Body Problem
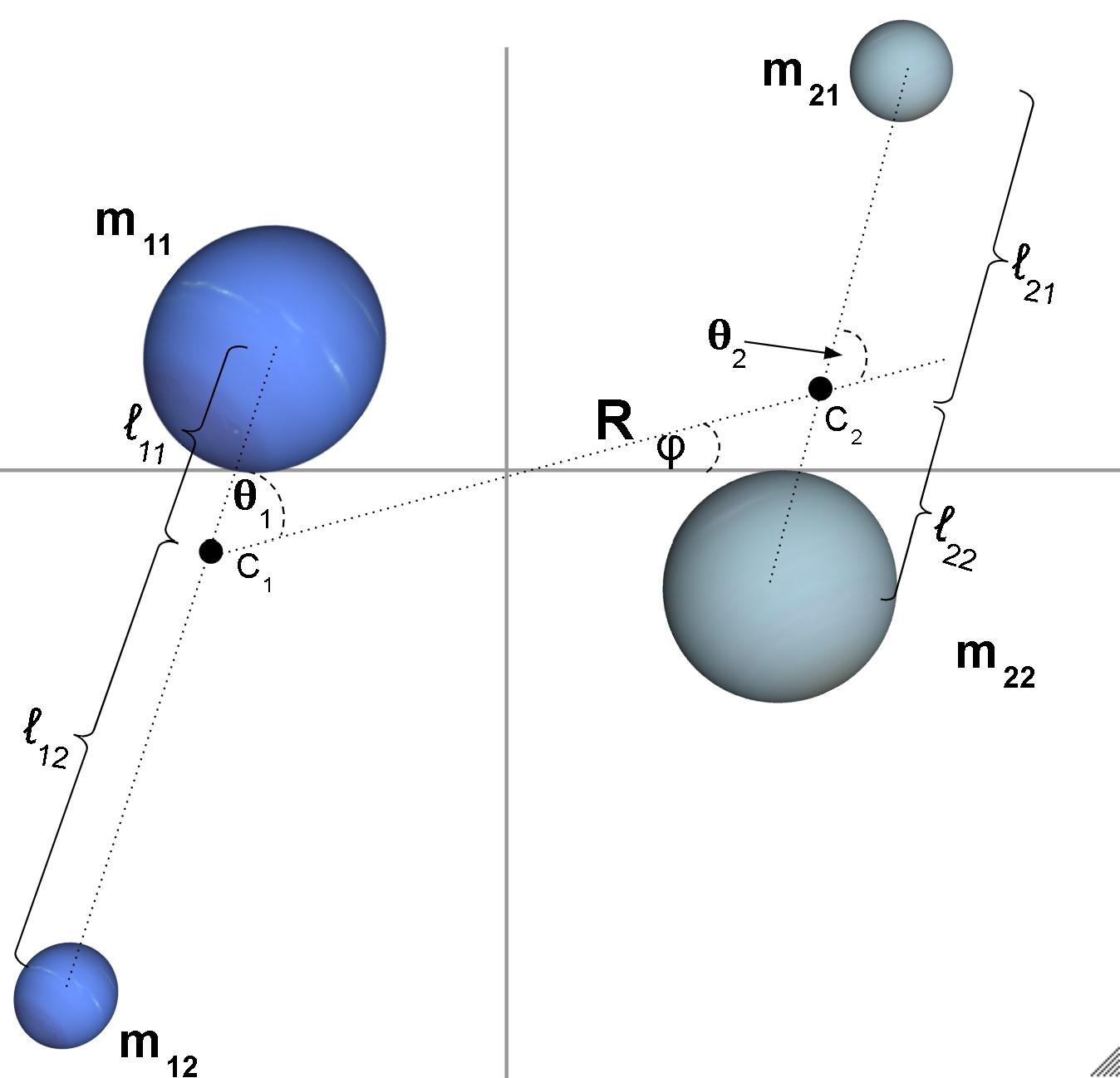 I work on the gravitational two body problem. In the cosmos, any two bodies share a gravitational attraction. When in proximity to one another, this attraction manifests in various celestial dances, which depends upon how they approach each other, their sizes, and their shapes. Their dance can end in several ways. They could join together to form a single body; they could fling themselves apart, never to see each other again; or they could find themselves in a perpetual dance. While Newton solved the case when these bodies are infinitely small, I examine the situation in which the bodies have various shapes and sizes. To do this, I use a model in which each of the two bodies is more complicated than just a round globe. Rather, each one is a collection of points connected to each other by rods. For example, an exercise dumbbell consists of two large masses connected by a rod, and this could be used to model an irregularly shaped asteroid. So imagine two such dumbbells in proximity to one another floating in space. What kind of dance will they perform? And why do we care? Practically speaking, many of the finite resources humans use on earth can be found in asteroids, many of which are irregular in shape. These irregular shapes can be modeled by masses connected by rods. And the calculations a spacecraft will need to make in oder to reach a stable orbit or "Relative Equilibria" around these asteroids will need to be based on gravitational models which take into account their irregular shapes. Finding these relative equilibria is the aim of my research.
I work on the gravitational two body problem. In the cosmos, any two bodies share a gravitational attraction. When in proximity to one another, this attraction manifests in various celestial dances, which depends upon how they approach each other, their sizes, and their shapes. Their dance can end in several ways. They could join together to form a single body; they could fling themselves apart, never to see each other again; or they could find themselves in a perpetual dance. While Newton solved the case when these bodies are infinitely small, I examine the situation in which the bodies have various shapes and sizes. To do this, I use a model in which each of the two bodies is more complicated than just a round globe. Rather, each one is a collection of points connected to each other by rods. For example, an exercise dumbbell consists of two large masses connected by a rod, and this could be used to model an irregularly shaped asteroid. So imagine two such dumbbells in proximity to one another floating in space. What kind of dance will they perform? And why do we care? Practically speaking, many of the finite resources humans use on earth can be found in asteroids, many of which are irregular in shape. These irregular shapes can be modeled by masses connected by rods. And the calculations a spacecraft will need to make in oder to reach a stable orbit or "Relative Equilibria" around these asteroids will need to be based on gravitational models which take into account their irregular shapes. Finding these relative equilibria is the aim of my research.
Black Hole Gravity Waves
 I'm also working to shine a light into black holes. Einstein taught us that when the universe gives birth to a black hole, it cries out with gravity waves. My colleagues and I calculate the "sound" that different types of black holes make at birth. A black hole's gravity waves are analogous to an earthquake's seismographic waves, they can be read as curvy lines on a page (called waveforms). A few years ago, scientists were finally able to detect gravity waves in this way. But what can we learn about black holes from looking at these waveforms? Can we determine the type or size of the black hole?
I'm also working to shine a light into black holes. Einstein taught us that when the universe gives birth to a black hole, it cries out with gravity waves. My colleagues and I calculate the "sound" that different types of black holes make at birth. A black hole's gravity waves are analogous to an earthquake's seismographic waves, they can be read as curvy lines on a page (called waveforms). A few years ago, scientists were finally able to detect gravity waves in this way. But what can we learn about black holes from looking at these waveforms? Can we determine the type or size of the black hole?
My colleagues and I take mathematical models (differential equations) representing black holes of different types, and then calculate the gravity waves predicted by these models. That way, when scientists detect gravity waves from space, one can compare those waveforms to those calculated from our research, and thereby determine the type of black hole which generated the waves. Additionally, since there is still much debate about the exact structure of black holes, we can compare the waveforms predicted by competing theories to determine which theory is correct.
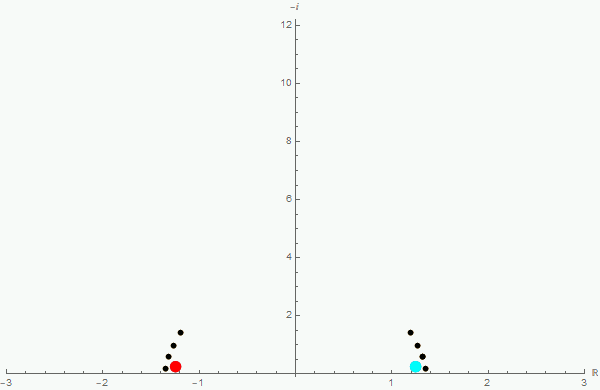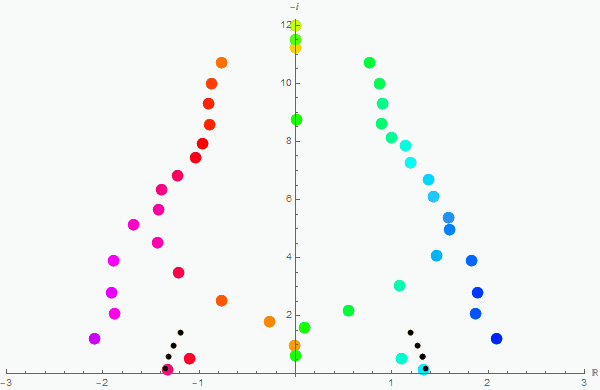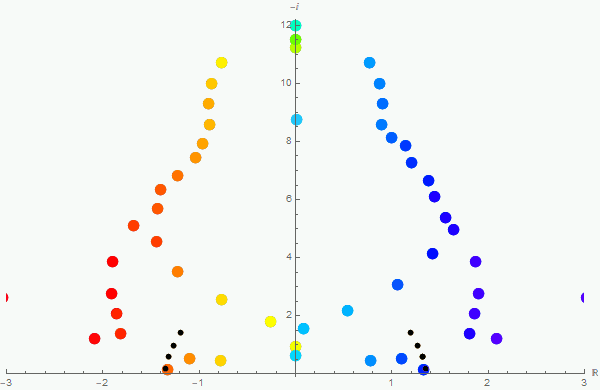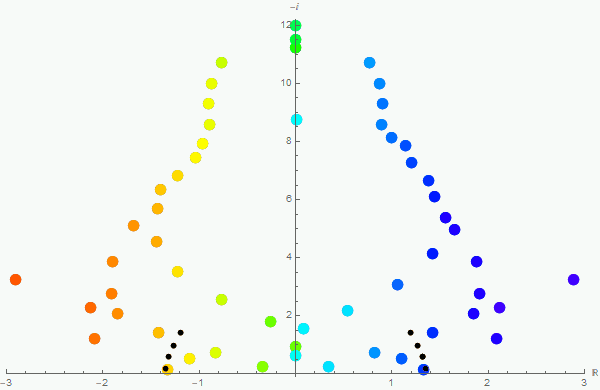
I have been researching gravity waves for a few years now. Back in 2017, I used a Taylor series method along with a recently published newer method to solve a gravity-wave related second-order homogeneous differential equation with boundary conditions. The differential equation has an irregular singular point, and is therefore resistant to many usual methods. Below, you will see a couple of animations I created using Mathematica. The first one is a result of the newer method in which I have expanded a Taylor series around each point in a grid in the domain. These expansions are then put in a system of equations in the form of a matrix, and then Cramer's rule is used to determine the derivatives of the function at each point. Finally, we find the determinant of the resulting coefficient matrix to approximate the allowed frequencies. This process is repeated for finer and finer grids within the domain. Each frame in the animation below represents approximations to the allowed frequencies (real part on the horizontal axis, and negative imaginary part on the upper part of the vertical axis). Each subsequent frame of the animation is the result of adding two additional points to the grid on the domain. The black dots represent known analytic solutions to this problem. Our hope is to expand the known solutions to higher-order frequencies.
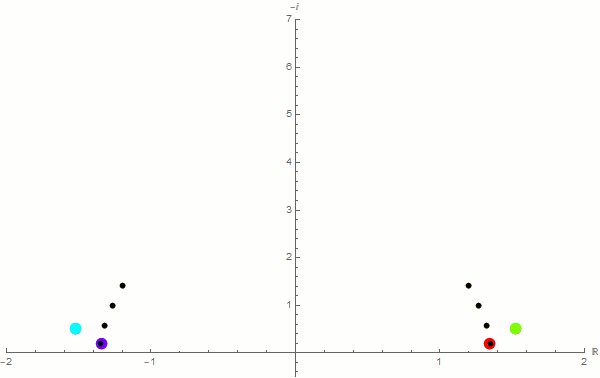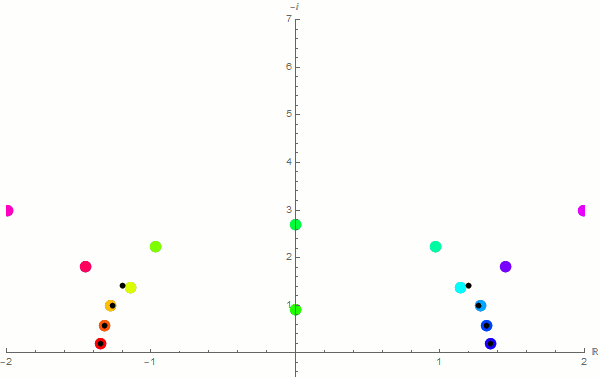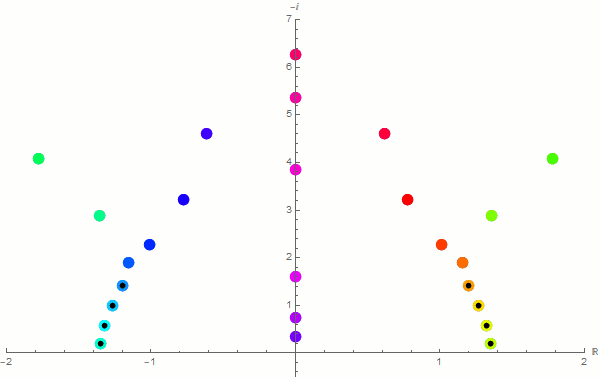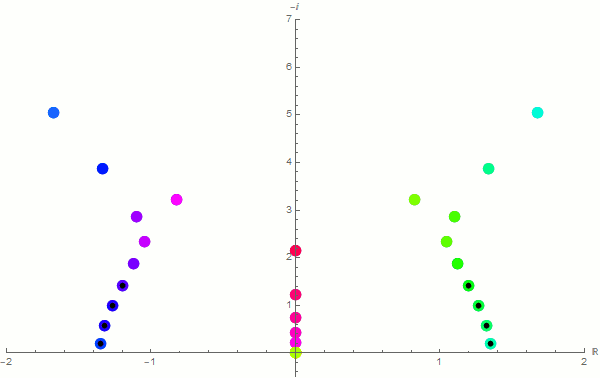
In the animation below, I've attempted the standard power series method, even though the irregular singular point does not guarantee the process will converge to functions with the desired frequencies. Each subsequent frame of the animation represents these approximations with an additional term in the Taylor expansion (with the last frame having 98 terms of the series). As you can see, most of the frequencies converge within a reasonable amount of time (as it relates to the ability of an average computer to process the expansion). Unfortunately, the values found do not agree with analytical results (unlike the previous example above), and is most likely attributable to the differential equation having an irregular singular point.
Environmental Sustainability
In early 2015, I presented results of research at the Joint Mathematics Meetings in San Antonio, Texas. I spoke at the MAA Contributed Papers Sessions, “Undergraduate Sustainability Experiences in the Mathematics Classroom.” I developed and published sustainability-related curriculum for college algebra and pre-calculus that will be made available to math teachers across the country through a National Science Foundation funded project called "Engaging Mathematics." This research resulted in two publications: one comparing the greenhouse gases produced by various automobile fuel choices, and the other exploring the impact of farming practices on the monarch butterfly.
